| หน้าแรก
| สารบัญ | โครงงาน
| การประกอบ
| การบัดกรี
|
เรียนอิเล็กทรอนิกส์
| อุปกรณ์
| 555 | สัญลักษณ์
| ถามบ่อยๆ
| ลิ้งค์ที่น่าสนใจ
| กลับไอซีอี
|
 หากจะมีส่วนให้ความรู้ให้ประโยชน์ต่อท่านบ้าง
ติชม เสนอแนะ
ถามปัญหา
ได้ที่
ice@icelectronic.com จะขอบคุณยิ่ง
หากจะมีส่วนให้ความรู้ให้ประโยชน์ต่อท่านบ้าง
ติชม เสนอแนะ
ถามปัญหา
ได้ที่
ice@icelectronic.com จะขอบคุณยิ่ง
เกทตรรกะ(Logic Gates)
ชนิดของเกท: NOT | AND | NAND
| OR | NOR | EX-OR | EX-NOR
สัญลักษณ์ | ตารางความจริง | ไอซีตรรกะ | สรุปของตารางความจริง | เกทผสม
| เกทแทน
หน้าต่อไป:
ค่าความจุและการใช้ตัวเก็บประจุ
ควรดู: ไอซีตรรกะ(Logic
ICs) | อนุกรม(Series)4000
| อนุกรม(Series)74
ด้วย
บทนำ
สภาวะตรรกะ
(Logic states) |
จริง
(True) |
ไม่จริง
(False) |
| 1 |
0 |
สูง
(High) |
ต่ำ
(Low) |
| +Vs |
0V |
เปิด
(On) |
ปิด
(Off) |
เกทตรรกะเป็นกระบวนการสร้างสัญญาณซึ่งแสดงถึงค่า
จริง(true)
หรือ ไม่จริง(false)
ปกติแหล่งจ่ายไฟบวก
+Vs แทนจริง(true)
และ 0V
แทนไม่จริง(false)
คำอื่นๆที่ใช้สำหรับสภาวะ
จริงและไม่จริงดังแสดงในตารางขวามือ
ซึ่งเป็นการดีที่จะทำความคุ้นเคยกับทั้งหมด เราระบุชื่อเกทจากฟังก์ชั่นการทำงานของมันได้แ่ก่: NOT, AND,
NAND, OR, NOR, EX-OR
และ EX-NOR
ใช้ตัวพิมพ์ใหญ่เพื่อให้ชัดเจนว่าหมายถึงเกทตรรกะ
โปรดสังเกตว่าเกทตรรกะไม่จำเป็นต้องใช้เสมอไป
เพราะเราสามารถใช้ฟังก์ชั่นตรรกะง่ายด้วยสวิทช์หรือไดโอด
เช่น:
สัญลักษณ์เกทตรรกะ
สัญลักษณ์เกทตรรกะมีสองอนุกรมคือ:
-
สัญลักษณ์แบบดั้งเดิมจะมีรูปร่างที่โดดเด่นทำให้ง่ายต่อการจดจำจึงมีการใช้กันอย่างแพร่หลายในอุตสาหกรรมและการศึกษา
- สัญลักษณ์ของ IEC (International
Electrotechnical Commission) เป็นรูปสี่เหลี่ยมกับสัญลักษณ์ภายในเพื่อแสดงฟังก์ชั่นของเกท
แม้ว่าเป็นทางการแต่ก็ไม่ค่อยมีคนใช้
แต่เราต้องรับรู้
เพื่อประโยชน์ในบางกรณี
อินพุทและเอาท์พุท
 เกทมีสองอินพุทหรือมากกว่า,
ยกเว้นเกท NOT
ซึ่งมีอินพุทเดียวและเอาท์พุทเดียว
ปกติตัวอักษร
A, B, C
และอื่นๆใช้เป็นป้ายบอกอินพุท
และ Q เป็นป้าย
บอกเอาท์พุท
อย่างรูปเกทขวามือ
อินพุทอยู่ทางซ้ายและเอาท์พุทอยู่ทางขวา
เกทมีสองอินพุทหรือมากกว่า,
ยกเว้นเกท NOT
ซึ่งมีอินพุทเดียวและเอาท์พุทเดียว
ปกติตัวอักษร
A, B, C
และอื่นๆใช้เป็นป้ายบอกอินพุท
และ Q เป็นป้าย
บอกเอาท์พุท
อย่างรูปเกทขวามือ
อินพุทอยู่ทางซ้ายและเอาท์พุทอยู่ทางขวา
วงกลม (o)กลับกัน(inverting)
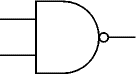 สัญลักษณ์เกทบางตัวมีรูปวงกลมเล็กๆอยู่ทางเอาท์พุท
ซึ่งหมายถึงรวมฟังก์ชั่นกลับกัน(inverting)ของเอาท์พุท
เทียบเท่ากับการป้อนเอาท์พุทผ่านเกท
NOT ตัวอย่าง
เช่นเกท NAND (Not AND)
ดังสัญลักษณ์ด้านขวามือ
เหมือนกับสัญลักษณ์เกท
AND
แต่เพิ่มวงกลมกลับกันที่เอาท์พุท
สัญลักษณ์เกทบางตัวมีรูปวงกลมเล็กๆอยู่ทางเอาท์พุท
ซึ่งหมายถึงรวมฟังก์ชั่นกลับกัน(inverting)ของเอาท์พุท
เทียบเท่ากับการป้อนเอาท์พุทผ่านเกท
NOT ตัวอย่าง
เช่นเกท NAND (Not AND)
ดังสัญลักษณ์ด้านขวามือ
เหมือนกับสัญลักษณ์เกท
AND
แต่เพิ่มวงกลมกลับกันที่เอาท์พุท
ตารางความจริง(Truth tables)
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
ตารางความจริงเป็นแนวทางที่ดีในการแสดงฟังก์ชั่นของเกทตรรกะ
แสดงสภาวะเอาท์พุทสำหรับทุกผลรวมที่เป็นไปได้ของสภาวะอินพุท
สัญลักษณ์ 0
(false) และ 1 (true)
มักใช้ในตารางความจริง
ตัวอย่างตารางความจริงด้านขวามือแสดงสภาวะอินพุทและเอาท์พุทของเกท
ANDด้านล่างมี สรุปตารางความจริง
แสดงสภาวะเอาท์พุทของเกททุกชนิดที่มีอินพุท
2 และ 3
ตารางนี้จะเป็นประโยชน์ในการช่วยเลือกเกทที่เหมาะสม
ไอซีตรรกะ(Logic ICs)
 เกทตรรกะสามารถหาได้ในรูปของไอซี(chips)
ซึ่งจะมีเกทแบบเดียวกันหลายเกทในไอซีหนึ่งตัว
ตัวอย่างเช่น
ไอซีเบอร์ 4001
ประกอบด้วยเกท
NOR 2 อินพุท 4 ตัว
ไอซีตรรกะมีหลายตระกูล
โดยสามารถแบ่งเป็นสองกลุ่มคือ:
ถ้าจะเปรียบเทียบความแตกต่างอย่างรวดเร็วโปรดดูที่:
เกทตรรกะสามารถหาได้ในรูปของไอซี(chips)
ซึ่งจะมีเกทแบบเดียวกันหลายเกทในไอซีหนึ่งตัว
ตัวอย่างเช่น
ไอซีเบอร์ 4001
ประกอบด้วยเกท
NOR 2 อินพุท 4 ตัว
ไอซีตรรกะมีหลายตระกูล
โดยสามารถแบ่งเป็นสองกลุ่มคือ:
ถ้าจะเปรียบเทียบความแตกต่างอย่างรวดเร็วโปรดดูที่:
ตระกูล 4000 และ 74HC
เหมาะสำหรับโครงงานที่ใช้ไฟแบตเตอรี่เลี้ยง
เพราะทำงานได้ดีกับแรงดันแหล่งจ่ายย่านนี้และกินไฟน้อย
อย่างไรก็ตาม
จงจำไว้ว่าในการใช้เกทตรรกะออกแบบวงจร
ต้องระวังว่าเกทที่ไม่ได้ใช้งานในวงจร
ทุกอินพุทที่ไม่ได้ใช้ต้องต่อกับแหล่งจ่ายไฟ
(อย่างใดอย่างหนึ่ง +Vs หรือ 0V)
เกท NOT (อินเวอเตอร์)
เอาท์พุท Q
เป็นจริงเมื่ออินพุท
A เป็นไม่จริง NOT
เอาท์พุทจะกลับกันกับอินพุท
: Q = NOT A
เกท NOT
มีเพียงอินพุทเดียว
เกท NOT
นี้บางทีเรียกว่าอินเวอเตอร์
 |
 |
| อินพุท A |
เอาท์พุท Q |
| 0 |
1 |
| 1 |
0 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
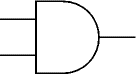
เกท AND
เอาท์พุท Q
เป็นจริงหากอินพุท
A AND อินพุท B
ทั้งคู่เป็นจริง: Q = A AND B
เกท AND
สามารถมีได้สองอินพุทหรือมากกว่า
เอาท์พุทเป็นจริงหากอินพุททั้งหมดเป็นจริง
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
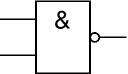
เกท NAND (NAND = Not AND)
คือเกท AND
ที่กลับเอาท์พุท
ดังที่มีวงกลม
'o'
ทางเอาท์พุท
เอาท์พุทเป็นจริงหากอินพุท
A AND กับ อินพุท B
เป็นไม่จริง: Q = NOT (A AND B)
เกท NAND
สามารถมีสองอินพุทหรือมากกว่า
เอาท์พุทเป็นจริงหากอินพุทไม่เป็นจริงทั้งหมด
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
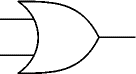
เกท OR
เอาท์พุท Q
เป็นจริงหากอินพุท
A OR อินพุท B
เป็นจริง (หรือทั้งคู่เป็นจริง): Q = A OR B
เกท OR
สามารถมีได้สองอินพุทหรือมากกว่า
เอาท์พุทเป็นจริงหากอย่างน้อยมีอินพุทหนึ่งเป็นจริง
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
เกท NOR (NOR = Not OR)
ก็คือเกท OR
ที่กลับเอาท์พุท
ดังที่มีเครื่องหมาย
'o'
ทางเอาท์พุท
เอาท์พุท Q
เป็นจริงหาก NOT
อินพุท A OR B
เป็นจริง: Q = NOT (A OR B)
เกท NOR
สามารถมีได้สองอินพุทหรือมากกว่า
เอาท์พุทเป็นจริงหากไม่มีอินพุทเป็นจริงเลย
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
เกท EX-OR (EXclusive-OR)
เอาพุท Q
เป็นจริงหากอินพุทอันใดอันหนึ่งคือ
A
เป็นจริงหรือ
OR อินพุท B
เป็นจริง
แต่ไม่หากอินพุททั้่งคู่เป็นจริง: Q = (A AND NOT B) OR (B AND NOT A)
เหมือนกับเกท
OR
แต่ไม่รวมอินพุททั้งคู่ที่เป็นจริง
เอาท์พุทเป็นจริงหากอินพุท
A และ B
มีสภาวะต่างกัน
เกท EX-OR
สามารถมีได้เพียงสองอินพุท
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
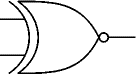
เกท EX-NOR (EXclusive-NOR)
ก็คือเกท EX-OR
ที่กลับเอาท์พุท
ดังที่มีเครื่องหมาย
'o'
ทางเอาท์พุท
เอาท์พุท Q
เป็นจริงหากอินพุท
A และ B
มีสภาวะเหมือนกัน
(เป็นจริงหรือไม่จริงทั้งคู่): Q = (A AND B) OR (NOT A AND NOT B)
เกท EX-NOR
สามารถมีได้สองอินพุท
 |
 |
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
| สัญลักษณ์เดิม |
สัญลักษณ์
IEC |
ตารางความจริง |
สรุปตารางความจริง
สรุปตารางความจริงด้านล่างแสดงสภาวะเอาท์พุทของเกททุกชนิดแบบสองอินพุทและสามอินพุท
| สรุปสำหรับเกท
2
อินพุททุกชนิด |
| อินพุท |
เอาท์พุทของเกทแต่ละชนิด |
| A |
B |
AND |
NAND |
OR |
NOR |
EX-OR |
EX-NOR |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
| สรุปสำหรับเกท
3
อินพุททุกชนิด |
| อินพุท |
เอาท์พุทของเกทแต่ละชนิด |
| A |
B |
C |
AND |
NAND |
OR |
NOR |
| 0 |
0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
1 |
1 |
0 |
| 1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
เกท EX-OR
และเกท EX-NOR
สามารถมีอินพุทเพียง
2 เท่านั้น |
การผสมเกทตรรกะ
เกทตรรกะสามารถผสมกันเพื่อให้เกิดฟังก์ชั่นที่ซับซ้อนมากขึ้น
นอกจากนี้สามารถผสมกันเพื่อ
ทดแทน
เกทชนิดหนึ่งเป็นเกทชนิดอื่น
| อินพุท A |
อินพุท B |
เอาท์พุท Q |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
ตัวอย่างเช่น
เพื่อให้ได้เอาท์พุท
Q
เป็นจริงเฉพาะเมื่ออินพุท
A
เป็นจริงและอินพุท
B
เป็นไม่จริง
ดังแสดงในตารางความจริงด้านขวา
เราสามารถผสมเกท
NOT และเกท AND
ดังนี้:

Q = A AND NOT B
ฟังก์ชั่นการทำงานของเกทแบบผสม
เราสามารถใช้ตารางความจริงแสดงฟังก์ชั่นของเกทแบบผสม
| อินพุท |
เอาท์พุท |
| A |
B |
C |
D |
E |
Q |
| 0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
1 |
1 |
ตัวอย่างเช่น
ตารางความจริงด้านขวาแสดงเอาท์พุท
D และ E
จากตรงกลางและเอาท์พุท
Q
สุดท้ายของวงจรเกทผสมด้านล่าง.

D = NOT (A OR B)
E = B AND C
Q = D OR E = (NOT (A OR B)) OR (B AND C)
การใช้เกทชนิดหนึ่งแทนเกทอื่น
เกทตรรกะสามารถหาได้ในรูปแบบไอซี
ที่ปกติมีเกทชนิดเดียวกันหลายๆตัว
เช่น เกท NAND
สองอินพุทหรือเกท
NAND สามอินพุท
จะเป็นการสิ้นเปลืองมากหากเราต้องการใช้เพียงสองสามเกท
แต่ต้องใช้ไอซีตรรกะหลายชนิด
นอกจากว่าทั้งหมดเป็นชนิดเดียวกัน
และเพื่อหลีกเลี่ยงไม่ให้ต้องใช้ไอซีมากเกินไป
เราสามารถลดจำนวนเกทอินพุทหรือแทนชนิดของเกทเป็นเกทแบบอื่นได้

การลดจำนวนอินพุท
จำนวนอินพุทของเกทสามารถลดลงโดยต่อสองอินพุท(หรือมากกว่า)
เข้าด้วยกัน
รูปด้านขวาแสดงเกท
AND สามอินพุท
ต่อเป็นเกท AND
สองอินพุท

การทำเกท NOT จากเกท NAND หรือ NOR
การลดอินพุทเกท
NAND หรือ NOR
เหลืออินพุทเดียวกลายเป็นเกท
NOT
ดังรูปด้านขวาใช้เกท
NAND
สองอินพุทต่อรวมกัน
เกทอะไรก็สามารถสร้างจาก
NAND หรือ NOR เกท
ตลอดจนเกท NOT,เกท NAND
หรือเกท NOR
สามารถรวมกันเพื่อสร้างเกทชนิดอื่น
ทำให้สามารถสร้างวงจรจากเกทชนิดเดียว,
ทั้ง NAND หรือ NOR
ตัวอย่างเช่นเกท
AND ก็คือเกท NAND
แล้วก็เกท NOT (เพื่อยกเลิกฟังก์ชั่นกลับ)
น่าสังเกตว่าเกท AND
และ OR
ไม่สามารถใช้ทำเกทอื่นได้เพราะไม่มีฟังก์ชั่นกลับ(NOT) เมื่อต้องการเปลี่ยนชนิดของเกท,
เช่นเปลี่ยน OR
เป็น AND,
เราต้องทำสามสิ่งต่อไปนี้:
- กลับ (NOT)
แต่ละอินพุท
- เปลี่ยนชนิดของเกท
(OR เป็น AND, หรือ AND
เป็น OR)
- กลับ (NOT)
เอาท์พุท
ตัวอย่างเช่นเกท
OR
สามารถสร้างจากอินพุท
NOT ป้อนเข้าเกท
NAND (AND +
NOT)
เทียบเท่าเกท
NAND
ตารางข้างล่างแสดงการต่อเกท
NAND
ให้เทียบเท่ากับเกท
NOT, AND, OR และเกท NOR :
| เกท |
เทียบเท่าเกท
NAND |
| NOT |
 |
 |
| AND |
 |
 |
| OR |
 |
 |
| NOR |
 |
 |
ตัวอย่างการทดแทนเกทในวงจรตรรกะ
 วงจรเดิมใช้เกทต่างกันสามชนิดคือ: NOR, AND
และ OR
ซึ่งต้องใช้ไอซีสามตัว
(แต่ละตัวเป็นเกทต่างชนิดกัน)
วงจรเดิมใช้เกทต่างกันสามชนิดคือ: NOR, AND
และ OR
ซึ่งต้องใช้ไอซีสามตัว
(แต่ละตัวเป็นเกทต่างชนิดกัน)ออกแบบใหม่โดยใช้เกท NAND
อย่างเดียว
เริ่มต้นด้วยการแทนแต่ละเกทด้วยเกทเทียบเท่า
NAND
ดังแสดงด้วยแผนภาพด้านล่าง

 จากนั้นก็ลดความซับซ้อนของวงจรโดยตัดคู่เกท
NOT ที่ติดกัน (เครื่องหมาย X
)
ที่ตัดออกได้เพราะเกท
NOT
ตัวที่สองจะ
ยกเลิกการกระทำของเกท
NOT ตัวแรก
จากนั้นก็ลดความซับซ้อนของวงจรโดยตัดคู่เกท
NOT ที่ติดกัน (เครื่องหมาย X
)
ที่ตัดออกได้เพราะเกท
NOT
ตัวที่สองจะ
ยกเลิกการกระทำของเกท
NOT ตัวแรก
วงจรสุดท้ายดังแสดงด้านขวามือโดยใช้เกท
NAND ทั้งหมด
และต้องการไอซีเพียงสองตัว(ไอซีหนึ่งตัวมีสี่เกท)
ดีกว่าวงจร
เดิมที่ต้องใช้ไอซีสามตัว
(หนึ่งตัวต่อเกทหนึ่งชนิด)
การทดแทนเกท
NAND (หรือ NOR)
ไม่ใช่ว่าจะเพิ่มจำนวนเกทเสมอไป
แต่เมื่อมันเป็น(เช่นในตัวอย่างนี้)โดยการเพิ่มเพียง
เกทหนึ่งหรือสองตัว
แต่ประโยชน์ที่แท้จริงคือการลดจำนวนไอซี
โดยใช้เกทชนิดเดียว
หน้าต่อไป: ค่าความจุและตัวเก็บประจุ |
เรียนรู้อิเล็กทรอนิกส์
ไอซีอีแปลและเรียบเรียง
เพื่อเผยแพร่สำหรับคนไทย
ผู้ที่มีอิเล็กทรอนิกส์ในหัวใจ
ขอขอบคุณ Mr. James Hewes






 หากจะมีส่วนให้ความรู้ให้ประโยชน์ต่อท่านบ้าง
ติชม เสนอแนะ
ถามปัญหา
ได้ที่
ice@icelectronic.com จะขอบคุณยิ่ง
หากจะมีส่วนให้ความรู้ให้ประโยชน์ต่อท่านบ้าง
ติชม เสนอแนะ
ถามปัญหา
ได้ที่
ice@icelectronic.com จะขอบคุณยิ่ง






 เกทมีสองอินพุทหรือมากกว่า,
ยกเว้นเกท NOT
ซึ่งมีอินพุทเดียวและเอาท์พุทเดียว
ปกติตัวอักษร
A, B, C
และอื่นๆใช้เป็นป้ายบอกอินพุท
และ Q เป็นป้าย
บอกเอาท์พุท
อย่างรูปเกทขวามือ
อินพุทอยู่ทางซ้ายและเอาท์พุทอยู่ทางขวา
เกทมีสองอินพุทหรือมากกว่า,
ยกเว้นเกท NOT
ซึ่งมีอินพุทเดียวและเอาท์พุทเดียว
ปกติตัวอักษร
A, B, C
และอื่นๆใช้เป็นป้ายบอกอินพุท
และ Q เป็นป้าย
บอกเอาท์พุท
อย่างรูปเกทขวามือ
อินพุทอยู่ทางซ้ายและเอาท์พุทอยู่ทางขวา สัญลักษณ์เกทบางตัวมีรูปวงกลมเล็กๆอยู่ทางเอาท์พุท
ซึ่งหมายถึงรวมฟังก์ชั่นกลับกัน(inverting)ของเอาท์พุท
เทียบเท่ากับการป้อนเอาท์พุทผ่านเกท
NOT ตัวอย่าง
เช่นเกท NAND (Not AND)
ดังสัญลักษณ์ด้านขวามือ
เหมือนกับสัญลักษณ์เกท
AND
แต่เพิ่มวงกลมกลับกันที่เอาท์พุท
สัญลักษณ์เกทบางตัวมีรูปวงกลมเล็กๆอยู่ทางเอาท์พุท
ซึ่งหมายถึงรวมฟังก์ชั่นกลับกัน(inverting)ของเอาท์พุท
เทียบเท่ากับการป้อนเอาท์พุทผ่านเกท
NOT ตัวอย่าง
เช่นเกท NAND (Not AND)
ดังสัญลักษณ์ด้านขวามือ
เหมือนกับสัญลักษณ์เกท
AND
แต่เพิ่มวงกลมกลับกันที่เอาท์พุท เกทตรรกะสามารถหาได้ในรูปของไอซี(chips)
ซึ่งจะมีเกทแบบเดียวกันหลายเกทในไอซีหนึ่งตัว
ตัวอย่างเช่น
ไอซีเบอร์ 4001
ประกอบด้วยเกท
NOR 2 อินพุท 4 ตัว
ไอซีตรรกะมีหลายตระกูล
โดยสามารถแบ่งเป็นสองกลุ่มคือ:
ถ้าจะเปรียบเทียบความแตกต่างอย่างรวดเร็วโปรดดูที่:
เกทตรรกะสามารถหาได้ในรูปของไอซี(chips)
ซึ่งจะมีเกทแบบเดียวกันหลายเกทในไอซีหนึ่งตัว
ตัวอย่างเช่น
ไอซีเบอร์ 4001
ประกอบด้วยเกท
NOR 2 อินพุท 4 ตัว
ไอซีตรรกะมีหลายตระกูล
โดยสามารถแบ่งเป็นสองกลุ่มคือ:
ถ้าจะเปรียบเทียบความแตกต่างอย่างรวดเร็วโปรดดูที่:


























 วงจรเดิมใช้เกทต่างกันสามชนิดคือ: NOR, AND
และ OR
ซึ่งต้องใช้ไอซีสามตัว
(แต่ละตัวเป็นเกทต่างชนิดกัน)
วงจรเดิมใช้เกทต่างกันสามชนิดคือ: NOR, AND
และ OR
ซึ่งต้องใช้ไอซีสามตัว
(แต่ละตัวเป็นเกทต่างชนิดกัน)
 จากนั้นก็ลดความซับซ้อนของวงจรโดยตัดคู่เกท
NOT ที่ติดกัน (เครื่องหมาย X
)
ที่ตัดออกได้เพราะเกท
NOT
ตัวที่สองจะ
ยกเลิกการกระทำของเกท
NOT ตัวแรก
จากนั้นก็ลดความซับซ้อนของวงจรโดยตัดคู่เกท
NOT ที่ติดกัน (เครื่องหมาย X
)
ที่ตัดออกได้เพราะเกท
NOT
ตัวที่สองจะ
ยกเลิกการกระทำของเกท
NOT ตัวแรก